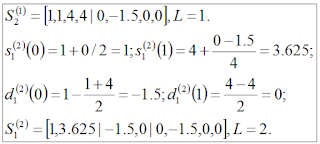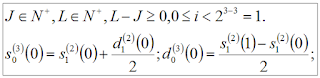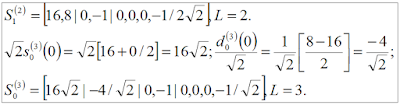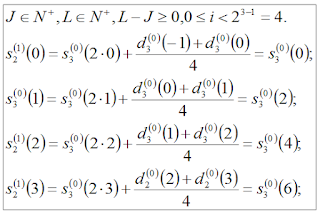This
post is a detailed example of computing individual elements of NCDF(S,
2, 2, L, 3) at each of the three scales on S = [1, 1, 1, 1, 4, 4, 4, 4]. NCDF(S, 2, 2, L, J) notation is
defined here. This notation is based on the notation introduced in Chapters 3 and 4 in "Ripples in Mathematics"
by A. Jensen & A. la Cour-Harbo.
Figures 1 and 2 show the formulas for the elements of S and D at scale L = 1. Figure 3 shows an example of computing the first scale of the signal S = [1, 1, 1, 1, 4, 4, 4, 4].
| Figure 1. Formulas for elements of S at scale L = 1 |
 |
| Figure 2. Formulas for elements of D at scale L = 1 |
 |
| Figure 3. Computing elements of S and D at scale L = 1 |
Figure 4 shows the individual formulas for S and D at scale L = 2. Figure 5 shows the computation of individual elements of S and D of the sample S = [1, 1, 1, 1, 4, 4, 4, 4] at scale L = 2.
 | |
| Figure 4. Formulas for elements of S and D at scale L = 2 |
 |
| Figure 5. Computing elements of S and D at scale L = 2 |
Figure 6 shows the individual formulas for S and D at scale L = 3. Figure 7 shows the computation of individual elements of S and D of the sample S = [1, 1, 1, 1, 4, 4, 4, 4] at scale L = 3.
 |
| Figure 6. Formulas for elements of S and D at scale L = 3 |
 |
| Figure 7. Computing elements of S and D at scale L = 3 |
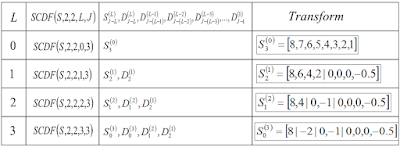
Figure 8 summarizes the three scales of NCDF(S, 2, 2, 3, 3), where S = [1, 1, 1, 1, 4, 4, 4, 4].
 |
| Figure 8. Summary of three scales of NCDF(S, 2, 2, 3, 3) on S = [1, 1, 1, 1, 4, 4, 4, 4] |